Dělení čísel
Dělení čísel je opačný proces k násobení čísel. Zároveň je dělení dobrým zdrojem humoru, protože, jak každý ví, nemůžeme dělit nulou, neboť by nám shořel sešit.
Co je to dělení čísel
Dělení si můžeme představit na příkladě rozdělení nějakého velkého celku na stejně velké menší dílky. Můžeme mít tatínka, který potřebuje rozřezat desku o délce 100 cm na pět stejně velkých dílů. Jak velké jednotlivé díly budou?
Můžeme postupovat naopak — pokud sečteme délky všech pěti uřezaných částí, musí nám vyjít zpátky číslo 100. Jaké číslo to splňuje? Je to číslo 20, protože 20 + 20 + 20 + 20 + 20 = 100. Místo sčítání můžeme použít i násobení. Můžeme se zeptat, jaké číslo po vynásobení pěti dá sto? Opět číslo 20, protože 5 · 20 = 100.
Graficky bychom to mohli vyjádřit jako rozdělení úsečky o délce 100 na pět stejně dlouhých částí:
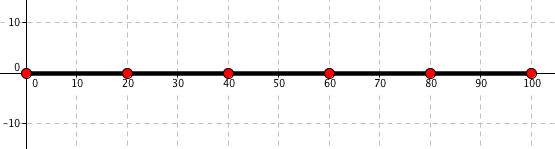
Pokud chceme vydělit číslo 100 číslem 5, zjišťujeme, „kolikrát se číslo pět vleze do čísla sto“. Dělení zapisujeme bud pomocí lomítka: 100 / 5 nebo pomocí dvojtečky: 100 : 5. Výsledkem dělení dvou čísel je podíl. V našich příkladech je číslo 20 podíl čísel 100 a 5. Číslo nalevo se nazývá dělenec, číslo napravo dělitel. Dělení můžeme také zapsat pomocí zlomku, místo 100 / 5 můžeme napsat $\frac{100}{5}$. Shrnutí názvosloví:
$$ a : b = \frac{a}{b} = c $$
- a se nazývá dělenec,
- b se nazývá dělitel,
- c se nazývá podíl.
Definice pomocí násobení
Podíl můžeme nejjednodušeji definovat pomocí násobení. Pro příklad si vezmeme podíl těchto čísel: 35 / 7. Jaký bude výsledek? My hledáme takové číslo, které když vynásobíme 7, tak získáme číslo 35. Kdybychom dělili 48 / 8, tak bychom hledali takové číslo, které by po vynásobení 8 dalo číslo 48.
Výsledkem 35 / 7 je tak číslo 5, protože 7 · 5 = 35. Výsledkem 48 / 8 je číslo 6, protože 8 · 6 = 48.
Pokud obecně dělíme a / b, pak výsledkem je číslo c, pro které platí b · c = a.
Ačkoliv jsme si všechny příklady ukazovali na přirozených číslech, tak díky definici pomocí násobení můžeme dělit i jakákoliv jiná čísla. Můžeme například najít podíl −85,76 / 6,7 tak, že najdeme číslo x, pro které platí 6,7 · x = −85,76. To platí pro x = −12,8.
Nulu můžeme podělit jiným číslem
Nulu můžeme podělit nějakým číslem, toto je platný výraz: 0 / 15. V podstatě tím říkáme, že chceme nulu rozdělit na 15 stejných částí. Můžeme si to představit tak, že nemáme žádný koláč a tento koláč, který nemáme, chceme rozdělit na 15 částí — jak velké budou jednotlivé části? Budou nulové, protože žádný koláč zkrátka nemáme. Případně si představte, že máte v peněžence nula korun a že chcete těchto nula korun rozdělit mezi tři děti. Kolik každé dítě dostane? Dostane kulové, protože zkrátka nic nemáte. Proto 0 / 15 = 0.
Dělit nulu jiným číslem můžeme, ale nemůžeme jiné číslo dělit nulou. Tento výraz je neplatný: 8 / 0.
Proč ale nemůžeme dělit nulou?
Dělit nulou nemůžeme, protože nám to zakazuje jedenácté přikázání.
Ale existují i pádnější důvody. Zatím se budeme zajímat o případ, kdy je dělenec různý od nuly — dělení je ve tvaru a / 0, kde a ≠ 0. Vyjmenujeme si dva důvody:
- Zkusme zůstat u analogie s rozdělením celku do menších, stejně velkých, částí. Máme 15, těch nejkrutějších, Pokémonů. Nyní je chceme rozdělit mezi nula dětí. Kolik každé dítě dostane Pokémonů?
Eh???
Ano, to zadání čtete správně a ano, nedává smysl. Nemůžeme se ptát, kolik Pokémonů dostalo každé dítě, když jsme neměli žádné dítě, kterému bychom ty Pokémony dali. Proto ani dělení nulou nedává smysl a proto říkáme, že výraz x / 0 je nedefinovaný.
- Dělení jsme si zavedli pomocí násobení. Když se pokoušíme dělit nulou 15 / 0, tak hledáme nějaké číslo x, pro které platí x · 0 = 15. Jenomže cokoliv krát nula je nula, nikdy nenajdeme x, pro které by tato rovnice měla smysl.
A co podíl 0/0?
Ten je nedefinovaný stejně jako x / 0. Důvody:
Tentokrát máme nula nejkrutějších Pokémonů, které chceme rozdělit mezi nula dětí. To je opět nesmyslný požadavek.
Dle definice dělení, když dělíme 0 / 0, tak hledáme takové číslo x, pro které platí x · 0 = 0. Řešení bychom našli, či přesněji: jakékoliv reálné číslo je řešením této rovnice. Ať už za x dosadíme 4, 1 nebo π, tak bude rovnice splněna. Samozřejmě je nepřípustné, aby výsledkem dělení byla celá množina reálných čísel, to nemá smysl.
Museli bychom z celé množiny vybrat jedno konkrétní číslo a říci, že právě toto číslo je výsledkem dělení 0 / 0. Jenže jaké? Mělo by se to rovnat jedné? Osmi? Nule? Minus jedné? A proč? Zkusíme si uvést argumenty pro nulu a pro jedničku:
- Víme, že pokud máme zlomek ve tvaru x / x, pak je tento zlomek roven jedné. Například 7 / 7 = 1 nebo 3 / 3 = 1. Odtud bychom mohli odvodit, že 0 / 0 bychom měli definovat tak, aby platilo 0 / 0 = 1.
- Podívejme se na tuto posloupnost jistě platných zlomků. V každém z nich budeme nulu dělit číslem, které se stále více a více blíží nule:
$$\begin{eqnarray} \frac{0}{1} &=& 0\\ \frac{0}{0{,}1} &=& 0\\ \frac{0}{0{,}01} &=& 0\\ \frac{0}{0{,}001} &=& 0\\ \frac{0}{0{,}0001} &=& 0\\ &…&\\ \frac{0}{0{,}0000000001} &=& 0\\ &…&\\ \frac{0}{0} &=& 0?\\ \end{eqnarray}$$
Vidíme, že ať dělíme číslem jakkoliv blízkým k nule, tak stále získáváme jako výsledek podílu nulu. Z toho bychom mohli odvodit, že 0 / 0 = 0.
Toto jsou oba platné argumenty, jak bychom mohli podíl 0 / 0 definovat. Jenže který z nich je lepší? Nakonec, i kdybychom jeden z nich zvolili a prohlásili za jediný platný, stejně bychom došli ke sporu s jinými částmi matematiky.
Proto je dělení nulou raději ponecháno jako nedefinované.
Finální argument proti dělení nulou
Pokud by vám předchozí argumenty nestačily, tak vás snad přesvědčí následující fotodokumentace případu, kdy se někdo opravdu pokoušel dělit nulou:

