Vektorový součin

Vektorový součin je operace v prostou mezi dvěma vektory, která nám vrátí nový vektor, který je na tyto dva vektory kolmý.

Co je to vektorový součin

Vektorový součin je definován mezi dvěma vektory a pouze v prostoru. Výsledkem vektorového součinu, na rozdíl od skalárního součinu, je opět vektor. Výsledkem vektorového součinu vektorů $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$ je vektor $\vec{\mathbf{w}}$, který má tyto vlastnosti:

$$|\vec{\mathbf{w}}|=|\vec{\mathbf{u}}|\cdot|\vec{\mathbf{v}}|\cdot\sin\alpha,$$

kde α je úhel mezi vektory $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$. Dále je vektor $\vec{\mathbf{w}}$ je kolmý k oběma vektorům $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$. Výsledný směr se pak řídí pravidlem pravé ruky. Abychom odlišili vektorový součin od skalárního, používáme u vektorového znaménko ×: $\vec{\mathbf{u}} \times \vec{\mathbf{v}}$.

Na otázku je znázorněn možný vektorový součin $\vec{\mathbf{u}} \times \vec{\mathbf{v}}$. Výsledkem je vektor $\vec{\mathbf{w}}$, který je kolmý na oba vektory. Pohybujeme se v prostoru, takže vektory $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$ jsou v jedné rovině a vektor $\vec{\mathbf{w}}$ je na tuto rovinu kolmý.

Pokud je jeden vektor lineární kombinací druhého, pak platí, že jejich vektorový součin je rovný nulovému vektoru. To zachycuje případy, kdy oba vektory leží na jedné přímce. Pokud je alespoň jeden vektor nulový, pak je i výsledný součin nulový.

Jak zjistit souřadnice výsledného vektoru

Prozatím umíme spočítat velikost výsledného vektoru a směr. Praktičtější ovšem je, znát přímo souřadnice takového vektoru. Samotný vzorec vypadá takto:

$$u\times v=(u_2v_3-v_2u_3, u_3v_1-v_3u_1, u_1v_2-v_1u_2)$$

Tenhle vzorec se pamatuje celkem těžko, proto existuje pomůcka, jak si ho zapamatovat:

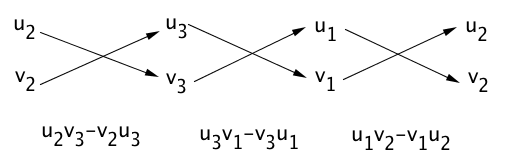
Pomocí této tabulku už můžeme vektory krásně násobit. Příklad: mějme vektory $\vec{\mathbf{u}}=(4,0,0)$ a $\vec{\mathbf{v}}=(0,5,0)$. Jedná se o vektory, které celé leží na ose x, respektive y. Jejich vektorový součin bude roven:

$$\begin{matrix} \vec{\mathbf{u}}&0&&0&&4&&0\\\hline \vec{\mathbf{v}}&5&&0&&0&&5\\ \vec{\mathbf{u}}\times \vec{\mathbf{v}}&&0&&0&&20 \end{matrix}$$

Výsledný vektor $\vec{\mathbf{w}}$ má souřadnice (0, 0, 20). Že je výsledek správný si můžeme ověřit podle první definice. Ta říká, že

$$|w|=|u|\cdot|v|\cdot\sin\alpha,$$

Náš vektor $\vec{\mathbf{w}}$ má velikost 20. Podle vzorce tak musí platit:

$$20=|u|\cdot|v|\cdot\sin\alpha$$

Dosadíme:

$$20=4\cdot5\cdot\sin90^\circ=20\cdot1=20.$$

K čemu je to dobré

Zřejmě můžeme pomocí vektorového součinu najít vektor, který je kolmý ke dvěma dalším vektorům. Že tomu tak skutečně je, si můžeme zase ověřit skalárním součinem. Výsledek musí být nula. Ověření pro předchozí příklad:

$$\begin{eqnarray} \vec{\mathbf{u}}\cdot \vec{\mathbf{w}}&=&4\cdot0+0+0\cdot20=0\\ \vec{\mathbf{v}}\cdot \vec{\mathbf{w}}&=&0+5\cdot0+0\cdot20=0 \end{eqnarray}$$

Další příklad použití je výpočet obsahu rovnoběžníku v prostoru. Máme-li rovnoběžník ABCD v prostoru a vektory $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$, které jsou tvořeny stranami AB a AD, pak obsah rovnoběžníku je roven $S=|\vec{\mathbf{u}} \times \vec{\mathbf{v}}|$. Máme-li v prostoru trojúhelník ABC, pak je jeho obsah rovný $S=\frac12|\vec{\mathbf{u}} \times \vec{\mathbf{v}}|$.

Příklad: vypočtěte obsah trojúhelníku v prostoru, který je tvořen vrcholy: A[1,0,3], B[5, 6, 8] a C[3, 5, 4].

Jako první si musíme určit vektory $\vec{\mathbf{u}}$ a $\vec{\mathbf{v}}$.

$$\begin{eqnarray} u&=&B-A=(4, 6, 5)\\ v&=&C-A=(2, 5, 1) \end{eqnarray}$$

Teď spočítáme jejich součin:

$$\vec{\mathbf{w}}=\vec{\mathbf{u}}\times \vec{\mathbf{v}}=(-19, 6, 8)$$

A následně velikost:

$$|\vec{\mathbf{w}}|=\sqrt{(-19)^2+6^2+8^2}=\sqrt{461}\approx21{,}47$$

A nakonec výsledek vydělíme dvěma:

$$S(\triangle ABC)=\frac{21{,}47}{2}=10{,}735$$