Směrnicový tvar přímky

Směrnicový tvar přímky vychází z velikosti úhlu, který svírá přímka s osou x.

Motivace

Máme přímku p, která má obecnou rovnici ax + by + c = 0. Víme, že grafem lineární funkce je právě přímka. Přitom lineární funkci jako takovou obvykle zapisujeme ve tvaru y = f(x). Mohli bychom tak chtít převést obecnou rovnici přímky ax + by + c = 0 právě na tento tvar. Abychom toho docílili, potřebujeme, aby b ≠ 0, protože potřebujeme z rovnice osamostatnit y a tedy celou rovnici vydělit b. Pokud tak b ≠ 0, můžeme obecnou rovnici upravit takto:

$$\begin{eqnarray} ax+by+c&=&0\qquad/ :b\\ \frac{ax}{b}+y+\frac{c}{b} &=&0\qquad/ \mbox{ osamostatníme }y\\ y&=&-\frac{ax}{b}-\frac{c}{b} \end{eqnarray}$$

Tím jsme získali zápis běžné lineární funkce. Protože je tento zápis docela složitý, provádíme nahrazení, takže položíme rovnosti

$$\begin{eqnarray} k &=& -\frac{a}{b}\\ q&=& -\frac{c}{b} \end{eqnarray}$$

a pak můžeme předchozí rovnici zapsat ve tvaru:

$$ y = kx+q $$

Není to žádný jiný tvar, jen jsme místo škaredého zlomku $-\frac{c}{b}$ napsali q, to je celé. Protože tvar kx + q popisuje běžnou lineární funkci, přímka v tomto tvaru nemůže být rovnoběžná s osou y. To jsme ostatně vyloučili už tím, že jsme řekli, že b ≠ 0.

Pokud by platilo, že b = 0, pak by přímka byla rovnoběžná s osou y a obecná rovnice takové přímky by měla tvar ax + c = 0. Pokud tuto rovnici vydělíme číslem a a upravíme, získáme:

$$\begin{eqnarray} ax + c &=& 0\qquad /:a\\ x + \frac{c}{a} &=& 0\\ x &=& -\frac{c}{a} \end{eqnarray}$$

Protože zlomek $-\frac{c}{a}$ je zase škaredý, zavádíme substituci $m = -\frac{c}{a}$, takže nakonec získáme rovnici

$$ x = m $$

Když to shrneme, každou přímku, která není rovnoběžná s osou y můžeme napsat ve tvaru y = kx + q, kde k, y ∈ ℝ a každou přímku rovnoběžnou s osou y můžeme napsat ve tvaru x = m, kde m ∈ ℝ.

Rovnici ve tvaru y = kx + y se pak říká směrnicový tvar přímky a koeficient k nazýváme směrnicí přímky.

Příklad

Máme přímku, která prochází body A[2, 8], B[8,10]. Určete směrnicový tvar přímky. Směrnicový tvar se nejlépe určuje z obecné rovnice přímky, takže nejprve sestrojíme ji. Obecná rovnice má tvar ax + by + c = 0, kde (a, b) je normálový vektor, takže nalezneme normálový vektor. Směrový vektor má souřadnice [8,10]−[2,8] = [6,2], takže normálový vektor $\vec{\mathbf{n}}$ má souřadnice [−2,6]. Do obecné rovnice tak můžeme dosadit a = −2, b = 6:

$$ -2x+6y+c=0 $$

Za souřadnice [x, y] dosadíme do rovnice nějaký bod, kterým přímka jistě prochází. Například bod B[8, 10]. Takže dosadíme do rovnice x = 8, y = 10:

\begin{eqnarray} -2\cdot8+6\cdot10+c&=&0\\ -16+60+c&=&0\\ c&=&-44\\ \end{eqnarray}

Vychází nám obecná rovnice

$$ -2x+6y-44=0 $$

Tuto rovici můžeme vydělit −2, získáme o trochu hezčí tvar:

$$ x-3y+22=0 $$

Směrnicový tvar získáme tak, že osamostatníme y. Převedeme všechny ostatní členy na pravou stranu a následně rovnici vydělíme třemi:

\begin{eqnarray} x-3y+22&=&0\\ -3y&=&-x-22\qquad/\cdot -1\\ 3y&=&x+22\qquad \cdot \frac13\\ y&=&\frac{1}{3}x+\frac{22}{3} \end{eqnarray}

Poslední řádek představuje přímku ve směrnicovém tvaru. Pokud bychom chtěli znát koeficienty k, q, zapsali bychom si $k=\frac13, q=\frac{22}{3}$. Ještě si můžete prohlédnout graf přímky se směrovým vektorem $\vec{\mathbf{u}}$ a normálovým vektorem $\vec{\mathbf{n}}$:

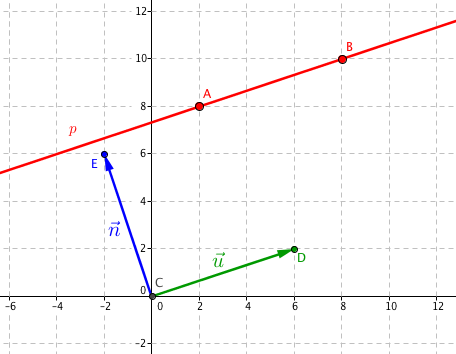
Pokud by nám zrovna koeficient q nevyšel tak nešikovně $\frac{22}{3}$, tak byste na první pohled viděli, že koeficient q určuje y-ovou souřadnici průsečíku přímky s osou y. Průsečík s osou y má x-ovou souřadnici x = 0. Když toto dosadíme do rovnice $y=\frac{1}{3}x+\frac{22}{3}$, dostaneme $y=\frac{1}{3}\cdot0+\frac{22}{3}=\frac{22}{3}$, tedy pro x = 0 má y hodnotu $y = \frac{22}{3}$.

Směrnice přímky

Máme-li rovnici přímky ve směrnicovém tvaru y = kx + q, pak číslu k říkáme směrnice přímky. Směrnice přímky má souvislost s úhlem, který svírá úsečka s kladnou poloosou x. Podívejte se na následující obrázek:

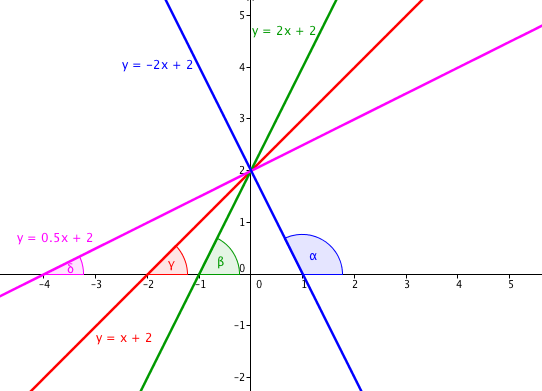
Obrázek zachycuje čtyři různé přímky s různými směrnicemi k, ale vždy se stejným koeficientem q = 2. Všechny přímky jsou tak ve tvaru y = qx + 2. Všimněte si, že jak se plynule mění hodnota směrnice, tj. číslo před neznámou x, tak se mění i úhel, který svírá přímka s kladnou poloosou x. Např. fialová přímka $y = \frac12x+2$ svírá s poloosou úhel δ, červená přímka y = x + 2 svírá s poloosou úhel γ a zelená přímka y = 2x + 2 svírá s poloosou úhel β.

V tomto případě platí, že čím větší je směrnice, tím větší je i úhel, který přímka s poloosou svírá. Směrnice fialové přímky $y = \frac12x + 2$ je $k_1 = \frac12$, směrnice zelené přímky y = 2x + 2 je k₂ = 2, platí tak k₁ < k₂. Zároveň platí, že δ < β. Ale např. směrnice modré přímky y = −2x − 2 je k₃ = −2, je tak menší než všechny předcházející a přitom úhel α je ze všech úhlů největší.

Vidíme, že směrnice k má s úhlem nějaký vztah. Prozkoumáme ho blíže. Zobrazíme si jen fialovou přímku $y = \frac12x+2$ a bude nás zajímat úhel δ. Zvolíme na přímce libovolné dva různé body A, B a vytvoříme z nich pravoúhlý trojúhelník ABC, jak je znázorněno na obrázku. Bude platit, že úhly δ a ε mají stejnou velikost, protože se jedná o souhlasné úhly.

Budeme se nyní snažit vyjádřit úhel ε za pomocí úseček AC a BC. Abychom to mohli udělat, potřebujeme znát délky těchto úseček. Označme si souřadnice bodů A a B takto: A = [x₁, x₂] = [2,3] a B = [x₂, y₂] = [6,5]. Délka úsečky AC tak bude rovnat rozdílu |x₂ − x₁| = |6 − 2| = 4. Vezmeme x-ovou souřadnici bodu B, která je shodná s x-ovou souřadnicí bodu C a odečteme od tohoto čísla x-ovou souřadnici bodu A. Tím získáme délku úsečky AC. Totéž uděláme s úsečkou BC, akorát vezmeme y-ové souřadnice. Platí tak |BC| = |y₂ − y₁| = |5 − 3| = 2.

Dále použijeme goniometrické funkce, konkrétně tangens. V pravoúhlém trojúhelníku ABC platí pro úhel ε, $\tan(\epsilon) = \frac{|BC|}{|AC|}$. Tangens úhlu ε je roven poměru protilehlé odvěsny ku přilehlé odvěsně. Pokud dosadíme za úsečky jejich vzdálenosti, získáme:

$$ \tan(\epsilon) = \frac{|BC|}{|AC|} = \frac{|y_2-y_1|}{|x_2-x_1|} = \frac{2}{4} = \frac12 $$

Tangens úhlu ε, který je stejný jako úhel δ, nám tak vyšel $\frac12$. Tangens úhlu, který svírá přímka s kladnou poloosou x je $\frac12$. Přitom rovnice této přímky je $y = \frac12x+2$, tedy tangens úhlu který svírá přímka s kladnou poloosou x je shodný se směrnicí této přímky! To není náhoda a platí to obecně:

Máme-li přímku p, která má směrnicovou rovnici y = kx + q, tak směrnice k je rovna tangentě úhlu, který svírá přímka p s kladnou poloosou x.

Odkazy a zdroje

• J. Polák: Přehled středoškolské matematiky