Normálový vektor přímky

Normálový vektor přímky p je vektor, který je kolmý k přímce p a jeho souřadnice vychází z obecné rovnice přímky.

Motivace

Máme přímku p, která prochází body A[0,1], B[2,5]. Přímka odpovídá grafu funkce y = 2x + 1, takže obecná rovnice přímky má tvar −2x + y − 1 = 0. Obrázek:

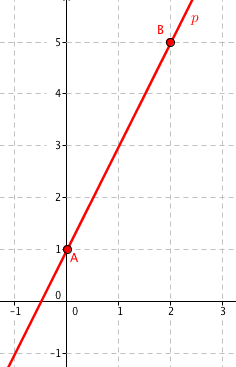
Obecná rovnice má obecný tvar ax + by + c = 0, v našem případě tak pro rovnici −2x + y − 1 = 0 platí a = −2, b = 1, c = −1. Jaký geometrický význam mají parametry a, b? Zkusíme si schválně jen tak pro zábavu nakreslit do obrázku vektor $\vec{\mathbf{u}}=(a, b)$, tj vektor $\vec{\mathbf{u}}=(-2,1)$:

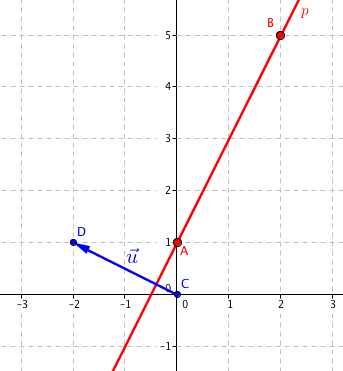
Poměrně jasně vidíme, že tento vektor je kolmý k přímce p. Není to náhoda, pokud bychom vzali jakoukoliv obecnou rovnici přímky ax + by + c = 0, tak vektor (a, b) by byl kolmý k této přímce. Takovému vektoru říkáme normálový vektor přímky p.

Vlastnosti normálového vektoru

Z vlastností skalárního součinu vektorů víme, že skalární součin dvou vektorů je nulový právě tehdy, když jsou na sebe vektory kolmé. Protože směrový vektor přímky p je rovnoběžný s přímkou p, tak to znamená, že jakýkoliv směrový vektor přímky p je kolmý k normálovému vektoru. Pokud spočítáme směrový vektor z úsečky $\vec{AB}$, dostaneme vektor

$$ \vec{\mathbf{v}} = B-A=[2{,}5]-[0{,}1]=[2{,}4] $$

Zakresleno v obrázku:

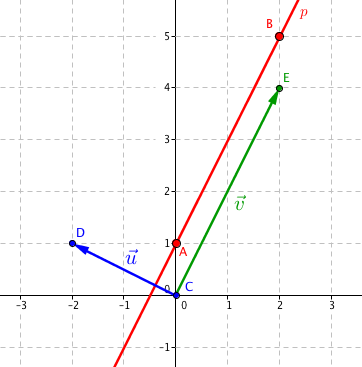
Když si trochu pohrajeme se skalární součinem dvou vektorů, který je pro připomenutí definovaný jako

$$(u_1, u_2) \cdot (v_1, v_2) = u_1\cdot v_1 + u_2 \cdot v_2,$$

tak zjistíme, že máme-li reálná čísla a, b, pak skalární součin vektorů (a, b) a (−b, a) a vektorů (a, b) a (b, −a) nám vždy vyjde nula:

$$\begin{eqnarray} (a, b)\cdot(-b, a) &=& a\cdot (-b) + b\cdot a = 0\\ (a, b)\cdot(b, -a) &=& a\cdot b - b\cdot a = 0\\ \end{eqnarray}$$

A teď se vraťme k přímce p danou obecnou rovnicí ax + by + c = 0 a k normálovému vektoru (a,b), který je kolmý k této přímce. Ale počkat! Přece díky předchozí vlastnosti víme, že vektory (−b, a) a (b, −a) mají s normálovým vektorem nulový skalární součin, takže vektory (−b, a) a (b, −a) musí být kolmé k normálovému vektoru! A protože normálový vektor je kolmý k přímce, tak vektor kolmý k tomuto vektoru musí být naopak rovnoběžný s původní přímkou p! Mazec!

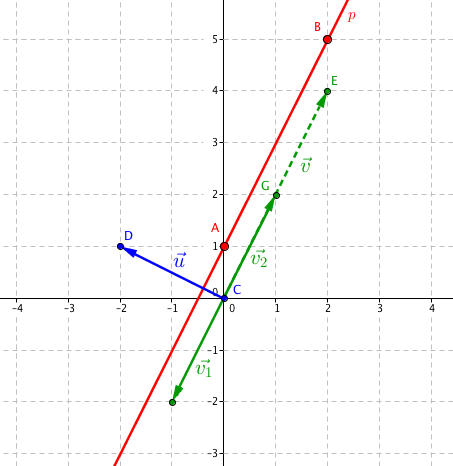
Můžeme si do obrázku zakreslit vektory $\vec{\mathbf{v}}_1=(-b, a)$ a $\vec{\mathbf{v}}_2=(b, -a)$. Přímka má obecnou rovnici −2x + y − 1 = 0, takže po dosazení máme zelené vektory $\vec{\mathbf{v}}_1=(-1, -2)$ a $\vec{\mathbf{v}}_2=(1, 2)$:

Určení obecné rovnice přímky z normálového vektoru a bodu

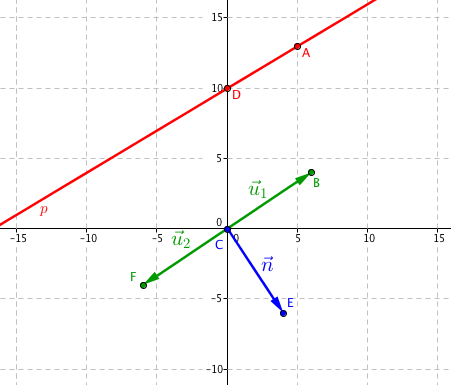
Už víme, že obecnou rovnici přímky můžeme celkem snadno vyjádřit z parametrické rovnice. Pokud známe normálový vektor $\vec{\mathbf{n}}$, můžeme obecnou rovnici také snadno určit. Takže mějme bod A[5,13], kterým přímka p prochází a její normálový vektor $\vec{\mathbf{n}}=(4,-6)$. Přímka p má obecnou rovnici ax + by + c = 0, z definice normálového vektoru přitom už můžeme hned určit koeficienty a, b, které se tak rovnají a = 4, b = −6, tj. souřadnicím normálového vektoru. Obecná rovnice přímky má tvar

$$ 4x-6y+c=0 $$

Zbývá nám dopočítat koeficient c. Tato rovnice popisující přímku p musí dávat smysl pro všechny body, které na přímce p leží. Což znamená, že když za x, y dosadíme souřadnice bodu, který leží na přímce p, rovnice musí být platná. Stačí tak dosadit bod A, kterým přímka p jistě prochází. Bod A má souřadnice A[5,13], takže do rovnice 4x − 6y + c = 0 dosadíme x = 5, y = 13:

$$\begin{eqnarray} 4\cdot5-6\cdot13+c&=&0\\ 20-78+c&=&0\\ c&=&78-20\\ c&=&58 \end{eqnarray}$$

Celá obecná rovnice přímky p má tak tvar

$$ 4x-6y+58=0. $$

Dva směrové vektory přímy p jsou $\vec{\mathbf{u}}_1=(6,4)$ a $\vec{\mathbf{u}}_2=(-6, -4)$.

Odkazy a zdroje

• J. Polák: Přehled středoškolské matematiky